MEDALIN TƏRS ÜZÜ

Dağ Üzü — Azərbaycan Respublikasıınn Yardımlı rayonunun inzibati ərazi vahidində kənd. == Tarixi == Dağ Üzü Yardımlı rayonunun Çay Üzü inzibati ərazi vahidində kənd. Peştəsər silsiləsinin yamacındadır. Keçmiş adı İlkin Üzü olunmuşdur. İnqilabdan əvvəl burada Üzü adlı bir kənd olmuşdur. Bu kənddən çıxmış ailələr sonralar çay sahilində yeni yaşayış məntəqəsi salmış və onu Çay Üzü adlandırmışdılar. Dağ yamacındakı əvvəlki Üzü kəndi isə Dağ Üzü adını almışdır.

Çay Üzü — Azərbaycan Respublikasının Yardımlı rayonunun inzibati ərazi vahidində kənd. Yardımlı rayonunun mərkəzindən təxminən 5 km cənub-qərbdə, Viləş çayının sahilində yerləşir. Çay Üzü kəndi Yardımlı rayonunun eyniadlı inzibati ərazi vahidində yerləşir. Viləş çayının sahilində, Talış dağlarının ətəyindədir. Toponim çay və Üzü (kənd adı) komponentlərindən düzəlib, "çay qırağındakı Üzü kəndi" deməkdir.

Səma — Yer səthindən yuxarıya doğru maneəsiz bir görünüş. Buraya atmosfer və kosmik fəza daxildir. O həm də yerlə kosmos arasındakı bölgə kimi də hesab olunur, buna görə də kosmosdan fərqlidir. Astronomiya sahəsində səmaya göy sferası da deyilir. Bu, Günəş, Ay, planetlər və ulduzların sürükləndiyi Yerə konsentrik olan mücərrəd sferadır. Göy sferası ənənəvi olaraq bürclər adlanan təyin olunmuş ərazilərə bölünür. Adətən "göy üzü" termini qeyri-rəsmi bir şəkildə Yer səthindən baxış bucağı kimi başa düşülür, amma mənası və istifadəsi fərqli ola bilər. Yer kürəsindəki bir müşahidəki gündüzlər gecəyə görə daha düz görünən bir günbəzə bənzəyən (bəzən göy kasası da deyilir) göy üzünün kiçik bir hissəsini görə bilər. Bəzi hallarda, məsələn, hava haqqında danışarkən, səma atmosferin yalnız aşağı, daha sıx təbəqələrini ifadə edir. Gündüz səması mavi görünür, çünki hava molekulları günəş işığının daha qısa dalğa uzunluqlarındakını daha uzun olanlara (qırmızı işıq) nisbətən daha çox səpələyir.

Tutaq ki, y = f ( x ) {\displaystyle y=f(x)} , x ∈ D ( f ) {\displaystyle x\in D(f)} ədədi funksiya verilmişdir. Onda hər bir x 0 ∈ D ( f ) {\displaystyle x_{0}\in D(f)} ədədinə yeganə y 0 = f ( x 0 ) ∈ E ( f ) {\displaystyle y_{0}=f(x_{0})\in E(f)} ədədi uyğundur. Funksiyanın verilən y 0 {\displaystyle y_{0}} qiymətinə görə arqumentin uyğun qiymətinin tapılmasına, daha doğrusu f ( x ) = y 0 {\displaystyle f(x)=y_{0}} , y 0 ∈ E ( f ) {\displaystyle y_{0}\in E(f)} tənliyinin x {\displaystyle x} -ə nəzərən həllinə tez-tez rast gəlinir. Həmin tənliyin bir yox, bir neçə və hətta sonsuz sayda həlli ola bilər. y = f ( x ) {\displaystyle y=f(x)} funksiyasının qrafiki ilə y = y 0 {\displaystyle y=y_{0}} düz xəttinin kəsişdiyi bütün nöqtələrin absisləri f ( x ) = y 0 {\displaystyle f(x)=y_{0}} tənliyinin Əgər f {\displaystyle f} funksiyası hər bir y 0 ∈ E ( f ) {\displaystyle y_{0}\in E(f)} qiymətini ancaq yeganə bir x 0 ∈ D ( f ) {\displaystyle x_{0}\in D(f)} qiymətində alırsa, onda o funksiya dönən adlanır. Belə funksiyalar üçün f ( x ) = y {\displaystyle f(x)=y} tənliyini istənilən y ∈ E ( f ) {\displaystyle y\in E(f)} qiymətində x-ə nəzərən birqiymətli həll etmək olar, daha doğrusu hər bir y ∈ E ( f ) {\displaystyle y\in E(f)} qiymətinə yeganə x ∈ D ( f ) {\displaystyle x\in D(f)} qiyməti uyğundur. Bu uyğunluq funksiya təyin edir, özü də f {\displaystyle f} funksiyasının tərsi adlanır və f − 1 {\displaystyle f^{-1}} simvolu ilə işarə olunur. Qeyd edək ki, hər bir y 0 ∈ E ( f ) {\displaystyle y_{0}\in E(f)} üçün y = y 0 {\displaystyle y=y_{0}} düz xətti dönən y = f ( x ) {\displaystyle y=f(x)} funksiyasının qrafikini yeganə ( x 0 , y 0 ) {\displaystyle (x_{0},y_{0})} nöqtəsində kəsir, burada f ( x 0 ) = y 0 {\displaystyle f(x_{0})=y_{0}} . Tərs funksiyanın arqumentini x {\displaystyle x} hərfi ilə, onun qiymətini isə – y {\displaystyle y} hərfi ilə işarə edərək, f {\displaystyle f} funksiyasının tərs funksiyasını y = f − 1 ( x ) , x ∈ D ( f − 1 ) {\displaystyle y=f^{-1}(x),x\in D(f^{-1})} , şəklində yazırlar. Sadəlik üçün f − 1 {\displaystyle f^{-1}} simvolu əvəzinə g {\displaystyle g} hərfindən istifadə edəcəyik.

Tərs matris — n tərtibli A kvadrat matrisinin tərsi elə bir B matrisinə deyilirki, A B = B A = E n {\displaystyle AB=BA=E_{n}} şərti ödənilsin. Burada En, n tərtibli vahid matrisdir. E n = ( 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 1 ) {\displaystyle E_{n}={\begin{pmatrix}\mathbf {1} &\mathbf {0} &\cdots &\mathbf {0} \\\mathbf {0} &\mathbf {1} &\cdots &\mathbf {0} \\\vdots &\vdots &\ddots &\vdots \\\mathbf {0} &\mathbf {0} &\cdots &\mathbf {1} \\\end{pmatrix}}} Tərs matrisi B=A−1 kimi işarələyirlər. Buradan belə nəticəyə gəlmək olar ki, A A − 1 = A − 1 A = E n {\displaystyle A{A^{-1}}=A^{-1}A=E_{n}} bərabərlik şərti ödənilməlidir.

Tərs qəfəs-mücərrəd üçölçülü bir fəzada qurulmuş nöqtəvi qəfəsdir. Bunun hansı fəzada necə qurulduğunu və ümumiyyətlə nəyə yaradığını yaxşı anlamaq üçün tərs qəfəs anlayışının bərk cisimlər fizikasındakı roluna nəzər salaq. Kristallik bərk cisimlərin bütün fiziki xassələri, əsas etibarı ilə iki faktor əsasında formalaşır. Bunlardan biri bərk cismi təşkil edən atomların quruluşu, ikincisi isə bərk cisimlərin öz kristal quruluşudur. Bir bərk cismin kristal quruluşa sahib olması nəzəri problemlərin həllində xüsusi əhəmiyyət kəsb edir. Beləki bərk cismin fiziki xassəsini ifadə edən və koordinatın funksiyası olan hər bir fiziki kəmiyyət koordinatın üçölçülü periodik funksiyası olur. Bu o deməkdir ki, bir nəzəri məsələnin həlli üçün yazılacaq tənliklərin bərk cismi təşkil edən bütün atomlar üçün deyil, periodun müəyyən elədiyi oblastda yer alan atomlar üçün yazılması kifayətdir. Period isə kristal qəfəsin köçürmə simmetriyasını müəyyən edən a → 1 , a → 2 , a → 3 {\displaystyle {\vec {a}}_{1},{\vec {a}}_{2},{\vec {a}}_{3}} vektorları ilə verilir. Bu vektorlara qəfəsin bazis vektorları və onların ədədi qiymətləri olan a , b , c {\displaystyle a,b,c} -lərə qəfəs sabitləri deyilir. Hər bir qəfəs üçün a → i {\displaystyle {\vec {a}}_{i}} vektorları üzərində qurulumuş paralepiped həmin qəfəsin elementar özəyi adlanır və onun həcmi V 0 = ( a → 1 [ a → 2 a → 3 ] ) {\displaystyle V_{0}={\Bigl (}{\vec {a}}_{1}[{\vec {a}}_{2}{\vec {a}}_{3}]{\Bigr )}} .

Tərs yer — Azərbaycan Respublikasının Gədəbəy rayonunun inzibati ərazi vahidində kənd. Azərbaycan Respublikası Milli Məclisinin 5 oktyabr 1999-cu il tarixli, 708-IQ saylı Qərarı ilə Gədəbəy rayonunun Samanlıq kənd inzibati-ərazi vahidi tərkibindəki yaşayış məntəqəsi Tərs yer kəndi adlandırılmış və rayonun yaşayış məntəqələri uçot məlumatına daxil edilmişdir. Kənd Kiçik Qafqaz dağlarının ətəyində, dağlıq ərazidə yerləşir. 2009-cu ilin siyahıyaalınmasına əsasən kənddə 138 nəfər əhali yaşayır. Əhalinin əsas məşğuliyyətini kənd təsərrüfatı — əkinçilik, maldarlıq və heyvandarlıq təşkil edir.

Tərs çay və ya Tərs çay qışlağı - Yelizavetpol (Gəncə) quberniyasının Qazax qəzasında, Dilican şəhəri yaxınlığında qışlaq. Tərsa çayının sahilində salındığı üçün yaşayış məntəqəsinin adı «Tərs çay qışlağı» adlandırılmışdır. Hidrotoponimdir. Quruluşca mürəkkəb toponimdir. 1897-ci ildə burada 10 nəfər azərbaycanlı, 18 erməni, 4 rus yaşamışdır. XX əsrin əvvəllərində ləğv edilmişdir.

Tərs A (böyük Ɐ, kiçik ɐ, riyazi simvol ∀) – A hərfinin tərsinə çevrilməsi ilə yaranan hərf və simvol. ɐ hərfi beynəlxalq fonetik əlifbada istifadə olunan simvollardan biridir. ∀ simvolu riyaziyyatda universal kvantifikasiyanı bildirmək üçün istifadə olunan məntiq simvoludur və "hamısı üçün" kimi tərcümə olunur. İlk dəfə Qerhard Qentsen tərəfindən 1935-ci ildə istifadə olunmuşdur. O, ilk dəfə Cüzeppe Peano tərəfindən istifadə olunmuş Ǝ simvolundan ilhamlanmışdır. Tərs a hərfi Edvard Lluyd və Vilyam Prays tərəfindən Korn dili üçün fonetik simvol kimi istifadə olunmuşdur. Onların kitablarında Ɐ və ɐ simvolları istifadə olunmuşdur. Simvol XIX əsrdə riyaziyyatçı Çarlz Sanders tərəfindən məntiq simvolu kimi işlədilmişdir. 2023-cü ildə Azərbaycan ordusuna məxsus hərbi texnikanın üzərində yazılmış tərsinə A hərfi Ermənistanda Zəngəzur dəhlizinə müdaxilənin simvolu kimi qiymətləndirilsə də, Azərbaycan tərəfi bu simvolun sadəcə digər ölkəyə aid maşınlardan fərqləndirmək üçün istifadə olunduğunu bildirmişdir. Akrofoniya prinsipinə görə A hərfi protosinan yazısında öküz (alef) başını təmsil edən simvoldan yaranmışdır.

Tərsinə mühəndislik — deduktiv mülahizə vasitəsilə əvvəllər hazırlanmış cihazın, prosesin, sistemin və ya proqram təminatının bir tapşırığı necə yerinə yetirdiyinin (əgər varsa) başa düşülməyə çalışıldığı proses və ya üsul. Nəzərdən keçirilən sistemdən və istifadə olunan texnologiyalardan asılı olaraq, tərsinə mühəndislik zamanı əldə edilən biliklər köhnəlmiş obyektlərin təyinatının dəyişdirilməsinə, təhlükəsizlik analizinin aparılmasına və ya bir şeyin necə işlədiyini öyrənməyə kömək edə bilər. Prosesin həyata keçirildiyi obyektə xas olmasına baxmayaraq, bütün tərsinə mühəndislik prosesləri üç əsas addımdan ibarətdir: məlumatın çıxarılması, modelləşdirmə və nəzərdən keçirmə. Məlumat çıxarma əməliyyat üçün bütün müvafiq məlumatların toplanması təcrübəsidir. Modelləşdirmə, yeni bir obyekt və ya sistemin layihələndirilməsi üçün bələdçi kimi istifadə edilə bilən abstrakt bir modeldə toplanmış məlumatların birləşdirilməsi təcrübəsidir. Nəzərdən keçirmə seçilmiş abstraktın etibarlılığını təmin etmək üçün modelin sınaqdan keçirilməsidir. Tərsinə mühəndislik kompüter mühəndisliyi, maşınqayırma, dizayn, elektron mühəndislik, proqram mühəndisliyi, kimya mühəndisliyi və sistem biologiyası sahələrində tətbiq olunur. Müxtəlif sahələrdə tərsinə mühəndisliyi yerinə yetirməyin bir çox səbəbi var. Tərsinə mühəndislik öz mənşəyini kommersiya və ya hərbi üstünlük üçün aparatların analizindən alır.:13 Bununla belə, tərsinə mühəndislik prosesi həmişə surətin yaradılması və ya artefaktın hansısa şəkildə dəyişdirilməsi ilə bağlı olmaya bilər.:15 Bəzi hallarda tərsinə mühəndislik prosesinin məqsədi sadəcə olaraq köhnə sistemlərin yenidən sənədləşdirilməsi ola bilər.:15 Hətta tərsinə çevrilmiş məhsul rəqibin məhsulu olsa belə, məqsəd onu kopyalamaq deyil, rəqibin analizini aparmaq ola bilər. Tərsinə mühəndislik qarşılıqlı fəaliyyət göstərən məhsullar yaratmaq üçün də istifadə edilə bilər və bəzi dar çərçivədə hazırlanmış ABŞ və Avropa İttifaqı qanunvericiliyinə baxmayaraq, bu məqsədlə xüsusi tərsinə mühəndislik üsullarından istifadənin qanuniliyi iyirmi ildən artıqdır ki, bütün dünyada məhkəmələrdə qızğın mübahisələrə səbəb olur.

Tərs Piramida (ing. PR – inverted pyramid) jurnalistikada, kopiraytinqdə və reklam yazarlığında tez-tez istifadə olunan termindir. Akademik yazılardan fərqli olaraq xəbər və ya reklam mətnləri Düz piramida deyil, "Tərs Piramida" formatında yazılır. "Tərs Piramida" qaydasına görə, ən vacib informasiya mətnin əvvəlində, yəni ilk cümlədə verilir. Sonra mətnin təfərrüatı və sonda "background" (arayış) deyilən hissə əlavə olunur. Bu prinsip ilə yazılan mətnlər dərhal oxucunun diqqətini cəlb edir.[1] Xəbər və reklam mətnlərində ən vacib informasiya mətnin əvvəlində olmalıdır. Məhz bu prinsipə "tərs piramida" deyilir. Məktəb və universitetlərdə bizə mətnlərin sadədən mürəkkəbə doğru yazılmasını öyrədirlər. Mətnlər yüngül məlumatlardan başlanır, tədricən qəlizləşir. Bu, mətn yazılmasında "düz piramida" prinsipidir.

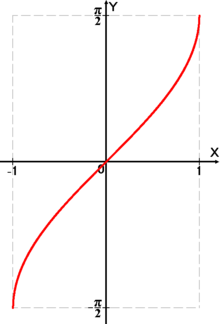
Tərs triqonometrik funksiyalar (dairəvi funksiya, arkfunksiya) — triqonometrik funksiyalar tərsinə çevrilə bilən riyazi funksiyalardır. Tərs triqonometrik funksiyalara əsasən altı funksiya daxildir: arksinus ( a r c s i n x {\displaystyle \mathrm {arcsin} \,x} — bu bucağın sinusu x {\displaystyle x} -ə bərabərdir) arkkosinus ( a r c c o s x {\displaystyle \mathrm {arccos} \,x} — bu bucağın kosinusu x {\displaystyle x} -ə bərabərdir) arktangens ( a r c t a n x {\displaystyle \mathrm {arctan} \,x} , bəzi ədəbiyyatlarda a r c t g x {\displaystyle \mathrm {arctg} \,x} ) arkkotangens ( a r c c o t x {\displaystyle \mathrm {arccot} \,x} və ya a r c c o t a n x {\displaystyle \mathrm {arccotan} \,x} , bəzi ədəbiyyatlarda a r c c t g x {\displaystyle \mathrm {arcctg} \,x} ) arksekans ( a r c s e c x {\displaystyle \mathrm {arcsec} \,x} ) arkkosekans ( a r c c s c x {\displaystyle \mathrm {arccsc} \,x} , bəzi ədəbiyyatlarda a r c c o s e c x {\displaystyle \mathrm {arccosec} \,x} ) Triqonometrik funksiyaların adının qarışındakı "arc" sözü ( lat. arcus — ox, qövs, qövsəoxşar xətt) bu funksiyaları tərs triqonometrik funksiyaların adına çevirir. Bu onunla bağlıdır ki, tərs triqonometrik funksiyaların həndəsi qiyməti vahid çevrənin qövsünün uzunluğu ilə əlaqələndirmək olar. Tərs triqonometrik funksiyalar anlayışını Laqranj köməyi ilə Avstriya riyaziyyatçısı Karla Şerfer (alm. Karl Scherffer‎; 1716—1783) daxil etmişdir. arcsin ⁡ x + arccos ⁡ x = π 2 {\displaystyle \arcsin x+\arccos x={\frac {\pi }{2}}} arctan x + arccot x = π 2 {\displaystyle \operatorname {arctan} \,x+\operatorname {arccot} \,x={\frac {\pi }{2}}} Arksinus - m ədədinin x bucağının qiymətinə , radian ifadəsinə deyilir, hansı ki, sin ⁡ x = m , − π 2 ⩽ x ⩽ π 2 , | m | ⩽ 1. {\displaystyle \sin x=m,\,-{\frac {\pi }{2}}\leqslant x\leqslant {\frac {\pi }{2}},\,|m|\leqslant 1.} y = sin ⁡ x {\displaystyle y=\sin x} funksiyası bütün ədəd oxunda kəsilməz və məhduddur. y = arcsin ⁡ x {\displaystyle y=\arcsin x} funksiyası ciddi artandır. sin ⁡ ( arcsin ⁡ x ) = x {\displaystyle \sin(\arcsin x)=x\qquad } − 1 ⩽ x ⩽ 1 , {\displaystyle -1\leqslant x\leqslant 1,} arcsin ⁡ ( sin ⁡ y ) = y {\displaystyle \arcsin(\sin y)=y\qquad } − π 2 ⩽ y ⩽ π 2 , {\displaystyle -{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}},} D ( arcsin ⁡ x ) = [ − 1 ; 1 ] {\displaystyle D(\arcsin x)=[-1;1]\qquad } (təyin oblastı), E ( arcsin ⁡ x ) = [ − π 2 ; π 2 ] {\displaystyle E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad } (qiymətlər çoxluğu).

Əsasən Sudanda yayılmışdır. Hündürlüyü 1 metr olan yarımkol və ya koldur. Yarpaqları 5 cüt, yarpaqcıqları enli, tərs-yumurtavari, ucdan dəyirmidir. Ləçəkləri qeyri bərabərdir. Paxlası yastı, oraqvari, iri, 3-4 sm uzunluğundadır. Avqust ayında çiçəkləyir. İşığa, istiyə, küləyədavamlı bitkidir. Torpağa tələbkar deyildir. Mədəni halda Abşeronda Dendrologiya İnstitutunun təcrübə sahəsində becərilir. Yolların kənarlarında canlı çəpərlərin salınmasında, qrup əkinlərində istifadəsi məqsədyönlüdür.

Üzü küləyə — 1977-ci ildə çəkilmiş Azərbaycan filmi. Film çoxplanlıdır. Burada dənizin çirklənməsi, Xəzərin balıq problemi və bir də quşların dövlət tərəfindən qorunması məsələlərinə toxunulmuşdur. Filmdə müasirlərimizin xarakterlərindən, onların mənəvi kamilliyindən, bir-birilərinə münasibətlərindən də söz açılır. Filmin qəhrəmanları gənclərdir. Onları inkişafımızın sabahı və gələcəyi düşündürür. İstər insanlara, istərsə də təbii sərvətlərə qayğı ilə yanaşan bu gənclər xalq malını dağıdanlara qarşı barışmazdırlar. Kinolent Mərkəzi televiziyanın (Moskva) sifarişi ilə çəkilmişdir. Ssenari müəllifi : Oqtay Orucov Quruluşçu rejissor : Əbdül Mahmudov Quruluşçu operator : Zaur Məhərrəmov Quruluşçu rəssam : Fikrət Əhədov Bəstəkar : Aqşin Əlizadə Səs operatoru : Vladimir Savin Montaj edən : Gülşən Səlimova Rejissor : Rafiq Yüzbaşov Operator : Amin Novruzov Adil İsgəndərov-Fərman Elxan Əhədzadə-Ramiz Tanilə Əhmərova-Nərgiz Muxtar Maniyev-Əbülfəz Əli Zeynalov-Əhməd dayı Kamal Xudaverdiyev-İlyas Məmmədov Həsən Məmmədov-Əlibala Zemfira Sadıqova-Nazlı xanım Kamil Məhərrəmov Zilli Namazov Azərbaycan Respublikası Mədəniyyət Nazirliyi. C.Cabbarlı adına "Azərbaycanfilm" kinostudiyası.

Tərs siyahılı verilənlər bazası ( ing. inverted list database ~ ru. база данных инвертированного списка ~ tr. ters listeli veritabanı) – relyasiyalı verilənlər bazasından aşağıdakı fərqləri olan verilənlər bazası: • Tərsinə çevrilmış siyahı cədvəlinin sətirləri (yazıları və ya kortejləri) hər hansı indeksləmə ardıcıllığından asılı olmayaraq müəyyən fiziki ardıcıllıqla yerləşir. • Ümumi verilənlər bazasını, bazanın cədvəlləri üçün qurulmuş müəyyən məntiqi birləşdirmə meyarlarından istifadə etməklə nizamlamaq olar. • Siyahının açarlarının sayı istənilən qədər ola bilər, həm də istər sadə, istərsə də mürəkkəb açarların əksinə olaraq, burada onlar istənilən sahə və ya sahələrin kombinasiyası ola bilər. • Bütövlüyə və ya unikallığa heç bir məhdudiyyət yoxdur. • Nə indekslər, nə də cədvəllər istifadəçiyə göstərilir. Belə verilənlər bazasının idarə olunması sistemindəki bu fərqlərə görə verilənlərin uzlaşmasını, bütövlüyünü və təhlükəsizliyini təmin etmək çox çətindir. İsmayıl Calallı (Sadıqov), “İnformatika terminlərinin izahlı lüğəti”, 2017, “Bakı” nəşriyyatı, 996 s.

Transformerlər 3: Ayın Qaranlıq Tərəfi (ing. Transformers: Dark of the Moon) — 2011-ci ildə istehsal olunmuş ABŞ filmi. Maykl Beyin rejissorluq etdiyi filmin baş rollarında Şaya LaBaf və Rouzi Hantinqton-Uaytli çəkilmişlər. Transformerlər: Məğlubların qisası filmin davamı. 1961-ci ildə avtobotlar və deseptikonlar arasındakı müharibəni bitirə biləcək bir kəşf daşıyan Saybetron kosmik gəmisi Ark vurularaq Ayın qaranlıq üzünə çırpılır. Qəza NASA tərəfindən aşkarlanır və ABŞ prezidenti Kenedi kosmik gəmini tədqiq etmək üçün Aya insan göndərmək təklifini qəbul edir. 1969-cu ildə Apollo-11 Aya enir və heyət Arkı araşdırmağa başlayır. Prezident Riçard Nikson bu tapşırığın detallarının gizli saxlanılması əmrini verir. Misir Müharibəsindən 3 il sonra Avtobotlar ABŞ ordusuna dünya miqyasında böyük toqquşmaları qabaqlamaq üçün kömək edir. Şühbəli yadplanetli texnologiyasını araşdırmaq üçün Ukraynanın Çernobil əyalətindəki bir əməliyyatda Deseptikon alim Şokveyv və nəhəng soxulcan robotu Driller tərəfindən hücuma məruz qalırlar.